Sie suchen einen zertifizierten Energieberater?
Letzte Aktualisierung: 11.03.2022
PV-Anlage: Bis zu 37% sparen!
Wir sparen für Sie bis zu 37% - durch unseren Experten-Vergleich!Jetzt Preise vergleichen!
Kinetische Energie berechnen & umrechnen: Definition, Formeln & Rechen-Beispiele
Definition: Kinetische Energie ist eine Energieform, die ein Körper in Bewegung besitzt. Sie entspricht dem Aufwand (Arbeit), der nötig ist, um das Objekt aus dem Ruhezustand in die momentane Bewegung zu bringen. Die kinetische Energie Ekin eines Körpers ist proportional zu seiner Masse m und proportional zum Quadrat seiner Geschwindigkeit v.
Fördermittel-Beantragung oder Sanierungsfahrplan?
Unsere geprüften Energieeffizienz-Experten übernehmen Ihren Förderantrag & erstellen Ihren Sanierungsfahrplan - zum Sparpreis!Jetzt Angebot anfordern!
Was ist kinetische Energie?
Die Physik versteht Energie als die Größe, die wegen der sogenannten Zeitinvarianz der Naturgesetze erhalten bleibt, wobei mit Zeitinvarianz die systemische Eigenschaft gemeint ist, dass bei gleicher Eingabe jederzeit das gleiche Verhalten gezeigt wird. Objekte, die Energie in sich tragen, sind sogenannte Energieträger bzw. Energiequellen.
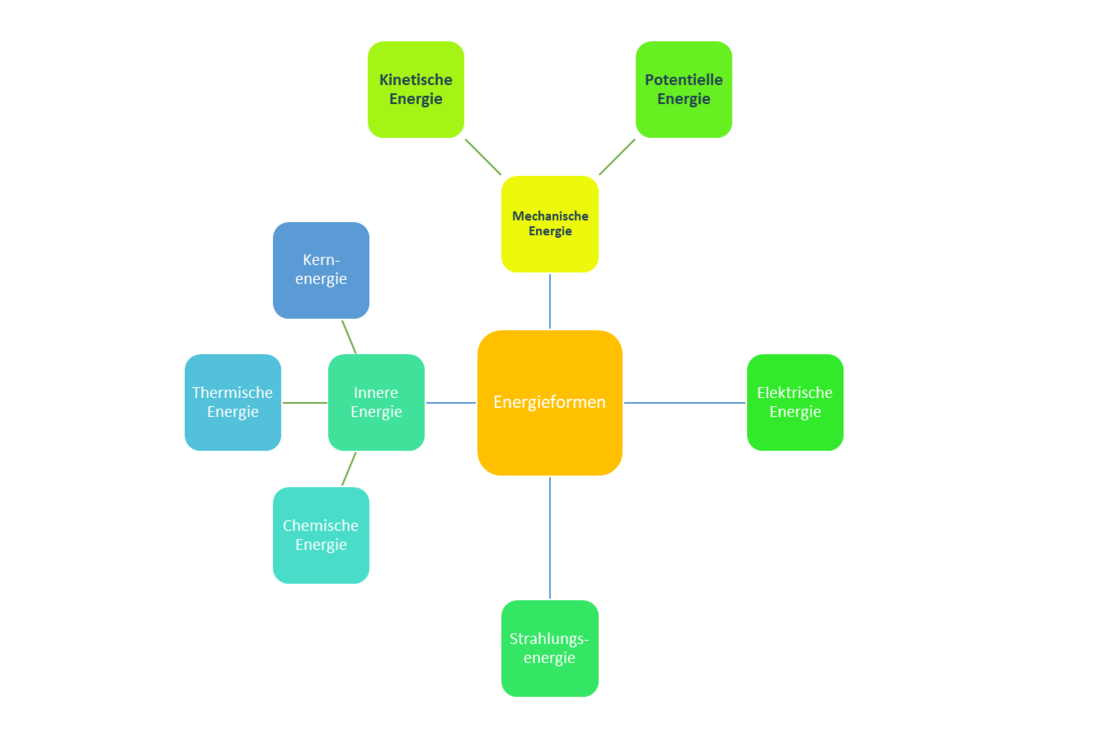
Daraus resultiert der sogenannte Energieerhaltungssatz, der besagt, dass sich die Gesamtenergie eines abgeschlossenen Systems weder vermehren noch vermindern lässt.
| Energieform | Beispiel |
|---|---|
| potentielle Energie (sogenannte Lageenergie) | Dachziegel |
| Rotationsenergie | Kreisel |
| chemische Energie | Wasserstoff |
| thermische Energie (sogenannte Wärmeenergie) | Kaminfeuer |
| Lichtenergie | Taschenlampe |
| magnetische Energie | Tafelmagnet |
| Kernenergie | Uranspaltung |
| kinetische Energie | fahrendes Auto |
Definition: So erklärt der Fachmann
Die sogenannte kinetische Energie mit dem Formelzeichen Ekin ist die Energie bzw. Energieform, die ein Objekt wegen seiner Bewegung besitzt.
Ein Körper bewegt sich, wenn er in einer bestimmten Zeitspanne seine Lage verändert. Der Fahrer eines Pkw zum Beispiel hat zum Pkw die kinetische Energie Null, zur Straße jedoch eine kinetische Energie größer Null. Die Umgebung wird somit zu einem Bezugssystem für den Körper.
Die kinetische Energie eines bewegten Körpers entspricht damit der Arbeit, die aufzuwenden wäre, um eben diesen bewegten Körper aus der Ruhe in die aktuelle Bewegung zu versetzen.
Die kinetische Energie ist somit ein Arbeitsvermögen, also ein Zustand bzw. eine Zustandsgröße. Deshalb ist die kinetische Energie in der klassischen Mechanik von
- der Masse (Gewicht) und
- der Geschwindigkeit (Tempo)
abhängig, die der bewegte Körper hat.
Es gilt: Mit steigender Masse und/oder Geschwindigkeit nimmt auch die kinetische Energie des Körpers zu.
Die kinetische Energie kann den Körper aber nicht nur zum Verrichten mechanischer Arbeit befähigen, sondern auch zur Abgabe von thermischer Energie oder Licht.
Maßeinheiten & Formel
Während Energie das physikalische Formelzeichen E zugeschrieben wird, gibt man die oben gelisteten Energieformen mit zusätzlichen tiefgestellten Buchstaben an. Ekin ist das Formelzeichen für die kinetische Energie.
Die einheitliche SI-Maßeinheit (SI = Système Internationale d'unités) für kinetische Energie ist Joule:
\(E_{kin} = 1 Joule := 1 {kg \cdot m^2 \over s^2} = 1Nm\)
m steht dabei für Meter, kg für Kilogramm, also der Masse des Körpers, und s für Sekunde, also die Dauer der Bewegung des Körpers. Zusammengefasst stehen diese Größen für die SI-Einheit Newtonmeter (Nm), die Energie und Arbeit im Verhältnis zueinander beschreiben.
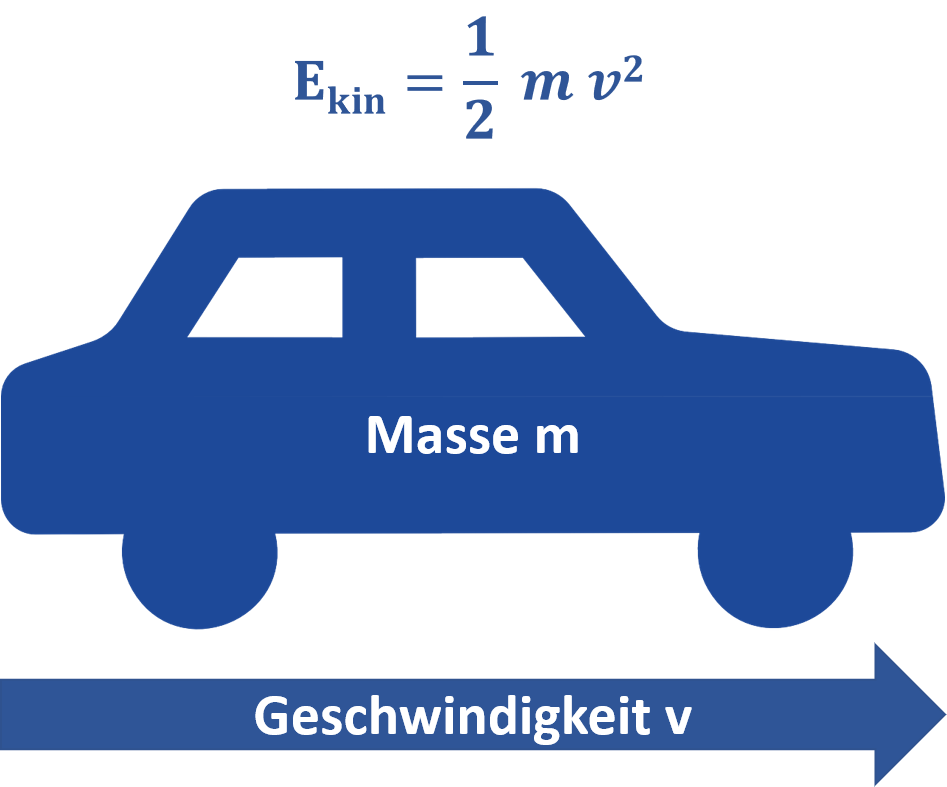
Wissenschaftler wie Gottfried Wilhelm Leibniz haben herausgefunden, dass die kinetische Energie Ekin eines Körpers proportional zu seiner Masse m und proportional zum Quadrat v2 seiner Geschwindigkeit ist.
Das konstante Verhältnis zu diesen beiden Größen wird als Proportionalitätskonstante bezeichnet, die in diesem Zusammenhang und Bedingungen den Wert ½ besitzt. Diese Konstante wurde u.a. bereits 1726 von Daniel Bernoulli beschrieben.
Mit der folgenden Formel kann die kinetische Energie eines sich in geradliniger Bewegung befindlichen Körpers berechnet werden:
\(E_{kin} = {1 \over 2} \cdot m \cdot {v^2}\)
Die kinetische Energie entspricht dann der Beschleunigungsarbeit, die aufgewendet werden müsste, um den Körper auf die Geschwindigkeit v zu bringen. Beim Abbremsen auf schließlich die Geschwindigkeit v = 0 wird die kinetische Energie wieder freigesetzt: als bei der stattfindenden Reibung entstehende Wärme oder als Verformung.
| Gegenstand | Masse | Geschwindigkeit | kinetische Energie in Joule |
|---|---|---|---|
| Apfel | 100 g | 1 m freier Fall | 1 J |
| Fußgänger | 55 kg | 5 km/h | 50 J |
| Radfahrer | 75 kg | 20 km/h | 1.200 J |
| PKW (Stadtverkehr) | 1.000 kg | 50 km/h | 96.000 J = 96 kJ |
| PKW (Landstraße) | 1.000 kg | 100 km/h | 386.000 J = 386 kJ |
| ICE | 500 t | 180 km/h | 625 MJ |
| Flugzeug (beim Start) | 320 t | 310 km/h | 1.200 MJ |
Beispiele zum Berechnen kinetischer Energie
Kinetische Energie begegnet uns überall im Alltag. Nachfolgend finden Sie die häufig im Physik-Unterricht gestellten Praxis-Aufgaben.
Einheiten umrechnen
Sehr anschaulich tritt kinetische Energie im Straßenverkehr auf. Verdoppelt man die Geschwindigkeit eines Fahrrades oder Autos von z. B. 25 Kilometer pro Stunde (km/h) auf 50 km/h, so vervierfacht sich die kinetische Energie. Dies ist u.a. bei der Abschätzung des nötigen Bremsweges entscheidend!
Beispiel-Aufgabe: Wie groß ist die Bewegungsenergie Ekin eines Autos, das 1 Tonne wiegt und 50 km/h schnell fährt?
Zum Berechnen dieser Aufgabe müssen zunächst die Einheiten von Tonnen in Kilogramm (kg) und die Geschwindigkeit km/h in Meter pro Sekunde (m/s) umgerechnet werden:
\(m = 1 Tonne = 1000 kg\)
\(v = 50 {km \over h} \cdot {1h \over 3600s} \cdot {1000m \over 1km} = 50 \cdot {1000m \over 3600s} = 50 \cdot {1 \over 3,6} {m \over s} \approx 13,88 {m \over s}\)
Formel lösen & ausrechnen
Zum Berechnen der Aufgabe werden nun lediglich diese Werte in die Formel eingesetzt und dann kann die Formel einfach ausgerechnet werden.
\(E_{kin} = {1 \over 2} \cdot m \cdot {v^2} = {1 \over 2} \cdot 1000kg \cdot (13,88 {m \over s}){^2} = 96,45 kJ\)
Lösung: Ein Auto, das 1 Tonne wiegt und 50 km/h schnell fährt, besitzt eine kinetische Energie von
\(96450 J = 96450 {kg m^2 \over s^2} = 96450 Nm\)
Formel umstellen: Geschwindigkeit und Gewicht berechnen
Nun lässt sich die Formel zur Berechnung der kinetischen Energie auch umstellen, um zum Beispiel die Geschwindigkeit oder das Gewicht eines Körpers zu berechnen, wenn die anderen Variablen der Formel bekannt sind.
Dann muss „lediglich“ die Formel nach der Geschwindigkeit v
\(E_{kin} = {1 \over 2} \cdot m \cdot {v^2}\)
\(E_{kin} = {m \cdot v^2 \over 2}\)
\(v = \sqrt {2 \cdot E_{kin} \over m}\)
oder dem Gewicht m umgestellt werden.
\(E_{kin} = {1 \over 2} \cdot m \cdot {v^2}\)
\(2 \cdot E_{kin} = {m \cdot v^2}\)
\(m = {2 \cdot E_{kin} \over v^2}\)
Ist die kinetische Energie und Gewicht des Autos bekannt, so lässt sich wie folgt die Geschwindigkeit berechnen:
\(v = \sqrt {2 \cdot E_{kin} \over m}\)
\(v = \sqrt {2 \cdot 96450 {kgm^2 \over s^2} \over 1000kg}\)
\(v = \sqrt {192,9 {m^2 \over s^2}}\)
\(v = 13,88{m \over s}\)
Ist die kinetische Energie und Geschwindigkeit des Autos bekannt, so lässt sich wie folgt das Gewicht berechnen:
\(m = {2 \cdot E_{kin} \over v^2}\)
\(m = {2 \cdot 96450 {kg m^2 \over s^2} \over {(13,88 {m \over s}})^2}\)
\(m = {2 \cdot 96450 \over 192,90} {kgm^2s^2 \over s^2m^2}\)
\(m = 1000kg\)
Umwandeln und umrechnen kinetischer Energie
Da Energie sich nur umwandeln lässt und nicht verloren gehen kann, gibt es auch unzählige Beispiele, wie sich kinetische Energie in eine andere Energieform umwandeln oder direkt nutzen lässt.
Ein Segel beispielsweise fängt die sich bewegende Masse Wind ein, so dass das zugehörige Schiff fortbewegt wird. Windkraftanlagen dagegen wandeln die kinetische Energie des Windes zunächst in Rotationsenergie um. Die Rotationsenergie wird genutzt, um einen Generator anzutreiben, der sie dann in elektrische Energie umwandelt - sprich: elektrischen Strom erzeugt. Dieser wird über Kabel durch den Turm der Windkraftanlage geführt und ins Stromnetz eingespeist.
Experten-Tipp: Beim sogenannten "Energy Harvesting" wird kinetische Energie mit Piezo-Zündern in Strom umgewandelt. Dies ist ermöglicht es, z.B. Funklichtschalter ohne Batterie oder Stromleitung mit Strom zu versorgen.
Potentielle in kinetische Energie umrechnen
Ein typisches Rechen-Beispiel aus dem Physik-Unterricht wird häufig durch einen Körper veranschaulicht, der fallen gelassen wird (wie die "Apfel-Anekdote", die man Isaac Newton nachsagt, der so das Prinzip der Schwerkraft erkannt haben soll), sodass potentielle Energie (Lageenergie) in kinetische Energie (Bewegungsenergie) umgewandelt wird.
Zur Umrechnung der potentiellen in kinetische Energie nutzt man daher zunächst die Ausgangs-Formel zur Berechnung der potentiellen Energie:
\(E_{pot} = {m \cdot g \cdot h}\)
M ist dabei die Masse, g die Geschwindigkeit bzw. Beschleunigung in Richtung Erde, die jeder Körper aufgrund seiner Gewichtskraft erfährt, die sogenannte Fallbeschleunigung, und h die Höhe aus die der Körper fallengelassen wird.
Die Fallbeschleunigung hat auf der Erde den Wert
\(g = 9,81 {m \over s^2}\)
Lässt man einen 3 kg schweren Körper aus 10.000 Metern Höhe fallen, so ergibt sich die dann resultierende kinetische Energie nachfolgender Rechnung:
\(E_{pot} = {m \cdot g \cdot h}\)
\(E_{pot} = 3kg \cdot 9,81 {m \over s^2} \cdot10000m\)
\(E_{pot} = 294300 {kg m^2 \over s^2}\)
Beim Fallen verringert sich also seine potentielle Energie und wandelt sich unmittelbar vor dem Auftreffen auf dem Boden (bei h = 0) vollständig in kinetische Energie um.
Die Umwandlung potenzieller Energie in kinetische Energie folgt damit dem Energieerhaltungssatz, nach dem die Gesamtenergie eines abgeschlossenen Systems bei allen Vorgängen konstant bleibt. Es gilt: Energie kann nur umgewandelt werden, aber nicht verloren gehen!
Daher kann man im Beispiel des freien Falls eines Körpers die potentielle Energie mit der kinetischen Energie gleichsetzen:
\(E_{kin} = E_{pot}\)
\({1 \over 2} \cdot m \cdot v^2 = m \cdot g \cdot h\)
Löst man nach v auf, so erhält man die gleiche Formel wie beim Auflösen/ Umstellen der Formel zur Berechnung der kinetischen Energie nach v:
\(v^2 = 2 \cdot g \cdot h\)
\(v = \sqrt{2 \cdot g \cdot h}\)
Kinetische in potentielle Energie umrechnen
Auf Grundlage dieser Zusammenhänge kann man natürlich auch berechnen, wie hoch ein Körper fliegt, wenn man ihn in die Luft wirft – sich also kinetische Energie am höchsten Punkt vollständig in potentielle Energie umgewandelt hat.
Die Höhe lässt wieder nach der bekannten Formel herleiten:
\(E_{kin} = E_{pot}\)
\({1 \over 2} \cdot m \cdot v^2 = m \cdot g \cdot h\)
\(h = {v^2 \over 2 \cdot g}\)
Wirft man einen Körper nun mit 15m/s senkrecht nach oben, so ergibt sich die Lösung aus folgender Berechnung:
\(x = {(15 {m \over s})^2 \over {2 \cdot 9,81{m \over s^2}}} = 11,47 m\)
Etwas komplexer wird die Rechnung, wenn man die Kugel von einer gespannten Feder abschießt. Die Kraft, die dann auf die Kugel wirkt ist die Spannenergie Espann, die mit folgender Formel berechnet wird:
\(E_{spann} = {1 \over 2} \cdot D \cdot s^2\)
Sie ist von der Federkonstante bzw. Federhärte D und ihrer Verlängerung („Spannung“) s abhängig.
Wird die Feder mit einer Federkonstanten von D = 15N/cm um s = 8cm gespannt, so wird die Spannenergie wie folgt berechnet:
\(E_{spann} = {1 \over 2} \cdot 1500 {N \over m} \cdot (0,08 m)^2 = 4,8 J\)
Da die Spannenergie der kinetischen Energie entspricht, gilt
\(E_{kin} = {1 \over 2} \cdot m \cdot v^2 = 4,8J\)
Nun kann man mit Hilfe dieser Formel wiederum die resultierende Geschwindigkeit der Kugel berechnen:
\(v = \sqrt {{2 \cdot E_{spann}} \over m} = \sqrt {{2 \cdot 4,8 J} \over 0,08 kg} = 10,95 {m \over s}\)
Da die kinetische Energie der Spannenergie entspricht, kann die Geschwindigkeit aber auch ohne vorherige Berechnung der Spannenergie aus folgender Formel abgeleitet werden:
\({1 \over 2} \cdot m \cdot v^2 = {1 \over 2} \cdot D \cdot s^2\)
\(v = \sqrt{{D \cdot s^2} \over m}\)
\(v = \sqrt{{1500 {N \over m} \cdot (0,08 m)^2} \over 0,08 kg} = 10,95 {m \over s}\)
Um die Höhe zu berechnen, die die Kugel erreicht, also die vollständige Umwandlung der kinetischen in potentielle Energie, kann wiederum die oben angeführte Formel angewendet werden:
\(E_{pot} = E_{kin}\)
\(m \cdot g \cdot h = {1 \over 2} \cdot m \cdot v^2\)
\(h = {v^2 \over 2 \cdot g} = {(10,95 {m \over s})^2 \over 2 \cdot 9,81{m \over s^2}} = 6,11 m\)
Letztlich gilt:
\(E_{pot} = E_{kin} = E_{spann}\)
Daher hätte die Höhe auch wie folgt berechnet werden können:
\(m \cdot g \cdot h = {{1 \over 2} \cdot D \cdot s^2}\)
\(h = {D \cdot s^2 \over 2 \cdot m \cdot g } = {1500 {N \over m} \cdot (0,08 m)^2 \over 2 \cdot 0,08 kg \cdot 9,81 {m \over s^2}} = 6,11 m\)
Eine interessante Kombination aus der Umwandlung potentieller in kinetischer und wieder in potentielle Energie stellt ein Fadenpendel dar. Alle Größen in den jeweiligen Zuständen können jedoch auch aus dem Zusammenhang
\(E_{kin} = E_{pot}\)
berechnet werden. Denn, ob man einen Körper senkrecht fallen lässt oder an einem Pendel schwingen lässt, ist zur Berechnung der Geschwindigkeit egal.
Solange die Reibung vernachlässigbar ist, hängt die erreichte Geschwindigkeit einzig und allein von der Höhendifferenz und damit von der Änderung der potentiellen Energie ab und nicht davon, auf welchem Weg der Körper die Höhendifferenz zurückgelegt hat.
Sanierungsprofis in Ihrer Nähe finden!
In wenigen Minuten Festpreis-Angebote für eine Dachsanierung, neue Fenster & Dämmung anfordern!Jetzt Preise vergleichen!
FAQ: Die häufigsten Fragen zur kinetischen Energie
Wie heißt die Formel der kinetischen Energie?
Die kinetische Energie Ekin eines Körpers ist proportional zu seiner Masse m und proportional zum Quadrat v² seiner Geschwindigkeit. Das konstante Verhältnis zu diesen beiden Größen beträgt ½. Die Formel für die kinetische Energie lautet daher Ekin = ½ ⋅ m ⋅ v²
Wie rechnet man kinetische in potenzielle Energie um?
Kinetische Energie ist Bewegungsenergie. Potentielle Energie ist hingegen Lageenergie. Verlangsamt sich ein Körper bis hin zum Stillstand, so wandelt sich die kinetische Energie vollständig in Lageenergie um. In diesem Fall werden beide Formeln gleichgesetzt, sodass man aus der kinetischen Energie die Variablen der potenziellen Energie berechnen kann und umgekehrt.
Welches Beispiel gibt es für kinetische Energie?
Sehr anschaulich tritt kinetische Energie im Straßenverkehr auf. Verdoppelt man die Geschwindigkeit eines Fahrrades oder Autos von z. B. 25 Kilometer pro Stunde (km/h) auf 50 km/h, so vervierfacht sich die kinetische Energie. Dies ist u.a. bei der Abschätzung des nötigen Bremsweges entscheidend!


